как работает gps, часть 1
Oct. 17th, 2009 10:51 pmЯ ж обещался написать, а.
Итак, все знают, что в небе, на полустационарной орбите (т.е. примерно 20 тыс км, период примерно 12 часов) летает до 30 спутников, под разными углами, так что отовсюду и всегда видно штук пять-десять.
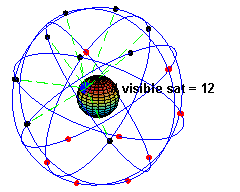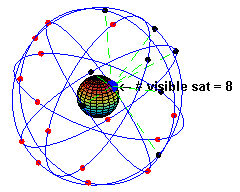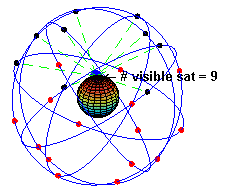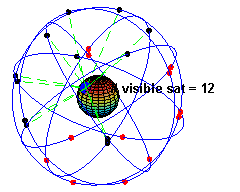
Все эти спутники шлют сигналы на как минимум двух частотах (L1=1575.42 MHz и L2=1227.60 MHz).
В вашем телефоне расположен чип (15 на 17 мм), и антенна, и этот чип ловит сигналы спутников, сколько именно, зависит от качества чипа.
Поймав эти сигналы, хитрый чип для каждого спутника расшифровывает положение спутника (передаётся в сигнале) и вычисляет расстояние до него. Так как наше пространство условно можно считать трёхмерным, то расстояния до четырёх опорных точек должно быть достаточно, чтобы узнать координаты точки.
В принципе, и трёх бы спутников хватило. Рисуем сферу радиуса R1 вокруг одного спутника, сферу радиуса R2 вокруг второго - в пересечении получается окружность; эта окружность пересекается со сферой радиуса R3 в двух точках; ну и эвристика подскажет, какая из двух. Даже и двух спутников хватит, если предположить, что мы находимся на поверхности Земли - вот вам и третья сфера.
Ну а если у нас больше чем три спутника, а, скажем, 5-8, то у нас много излишней информации, и мы можем очень хорошо избавиться от накапливающихся ошибок в вычислениях, используя Метод Наименьших Квадратов - т.е. вычислить точку, где суммарная квадратичная ошибка минимизируется. МНК удобная вещь, состоит в решении системы линейных уравнений, и даже в случае плохой, даже вырожденной матрицы есть очень миленькие методы, позволяющие найти решение.
Но тут у нас возникает два недоуменных вопроса:
а) как это мы на одной и той же частоте принимаем дикое количество сигналов, и не путаем, что от кого?
б) а как это по сигналу мы можем определить расстояние до спутника? Допплер? Но Допплер поможет измерить относительную скорость, а не расстояние.
Вот про это-то я и расскажу в следующих частях, а пока немножко беллетристики.
Из этих двух частот первая, L1, имеет общегражданское назначение, и даёт нам точность до трёх метров. L2, военная, помогает скорректировать результат до 30 см. Но это ещё что. До 2000-го года в сигнал L1 нарочно вводилась ошибка, снижающая точность до 10 метров по горизонтали и 30 по вертикали. Чтобы вражеские ракеты не ориентировались. А L2 как раз передавал поправку, но этот сигнал был зашифрован. Ну конечно ездить по Америке с точностью 10 метров не по кайфу, и поэтому на земле порасставлены станции DGPS, корректирующие сигнал. Эту ошибку отключали в 90-м, во время Gulf war, потому что в армии навигаторов не хватало, и они скупали гражданские - так чтоб не заблудились солдатики.
Ошибку должны были снять только к 2006-му году, но военные насобачились избирательно ставить ошибку, так что тогда же, 1-го мая 2000-го года, её и отменили.
Вообще, сейчас входит в моду устанавливать наземные станции GPS даже в зданиях, скажем, в аэропортах и в корпусах Гугла, чтобы можно было ориентироваться без всяких спутников и даже знать, на каком мы этаже, и показывать на телефоне план этажа.
Итак, все знают, что в небе, на полустационарной орбите (т.е. примерно 20 тыс км, период примерно 12 часов) летает до 30 спутников, под разными углами, так что отовсюду и всегда видно штук пять-десять.

Все эти спутники шлют сигналы на как минимум двух частотах (L1=1575.42 MHz и L2=1227.60 MHz).
В вашем телефоне расположен чип (15 на 17 мм), и антенна, и этот чип ловит сигналы спутников, сколько именно, зависит от качества чипа.
Поймав эти сигналы, хитрый чип для каждого спутника расшифровывает положение спутника (передаётся в сигнале) и вычисляет расстояние до него. Так как наше пространство условно можно считать трёхмерным, то расстояния до четырёх опорных точек должно быть достаточно, чтобы узнать координаты точки.
В принципе, и трёх бы спутников хватило. Рисуем сферу радиуса R1 вокруг одного спутника, сферу радиуса R2 вокруг второго - в пересечении получается окружность; эта окружность пересекается со сферой радиуса R3 в двух точках; ну и эвристика подскажет, какая из двух. Даже и двух спутников хватит, если предположить, что мы находимся на поверхности Земли - вот вам и третья сфера.
Ну а если у нас больше чем три спутника, а, скажем, 5-8, то у нас много излишней информации, и мы можем очень хорошо избавиться от накапливающихся ошибок в вычислениях, используя Метод Наименьших Квадратов - т.е. вычислить точку, где суммарная квадратичная ошибка минимизируется. МНК удобная вещь, состоит в решении системы линейных уравнений, и даже в случае плохой, даже вырожденной матрицы есть очень миленькие методы, позволяющие найти решение.
Но тут у нас возникает два недоуменных вопроса:
а) как это мы на одной и той же частоте принимаем дикое количество сигналов, и не путаем, что от кого?
б) а как это по сигналу мы можем определить расстояние до спутника? Допплер? Но Допплер поможет измерить относительную скорость, а не расстояние.
Вот про это-то я и расскажу в следующих частях, а пока немножко беллетристики.
Из этих двух частот первая, L1, имеет общегражданское назначение, и даёт нам точность до трёх метров. L2, военная, помогает скорректировать результат до 30 см. Но это ещё что. До 2000-го года в сигнал L1 нарочно вводилась ошибка, снижающая точность до 10 метров по горизонтали и 30 по вертикали. Чтобы вражеские ракеты не ориентировались. А L2 как раз передавал поправку, но этот сигнал был зашифрован. Ну конечно ездить по Америке с точностью 10 метров не по кайфу, и поэтому на земле порасставлены станции DGPS, корректирующие сигнал. Эту ошибку отключали в 90-м, во время Gulf war, потому что в армии навигаторов не хватало, и они скупали гражданские - так чтоб не заблудились солдатики.
Ошибку должны были снять только к 2006-му году, но военные насобачились избирательно ставить ошибку, так что тогда же, 1-го мая 2000-го года, её и отменили.
Вообще, сейчас входит в моду устанавливать наземные станции GPS даже в зданиях, скажем, в аэропортах и в корпусах Гугла, чтобы можно было ориентироваться без всяких спутников и даже знать, на каком мы этаже, и показывать на телефоне план этажа.